第４７章 マクローリン展開の基礎の基礎 　

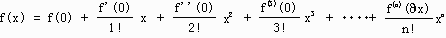
昔、筆者が高校の時マクローリン展開というのを 習ったことがあります。これは、驚きでした。 マクローリン展開というのは、数学的な厳密さを 無視して、直感的に分かりやすくいうと次のようになります。

n回微分可能な関数f(x)は次のように表すことができる

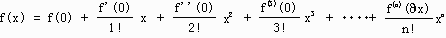
この式をよく見ると右辺の分数部分は単なる定数です。ということは 微分さえできれば、どんな関数でも 


f(x) = a + bx + cx2 + ････ (a,b,cは定数)
の形で表せるということです。しかも、階乗は急速に大きくなるので 右端へ行けば行くほど定数の値は限りなく０に近づくでしょう。 （数学的に今の表現が正しいかどうかわかりません。でも直感的に わかりますね。）

「それが、一体プログラミングとどー関係があるの？」

まー、もう少し我慢していてください。要するに、何回も 微分できる関数なら簡単な形に書き直せる（近似できる） という話です。では、具体的な例を見てみましょう。 微分しても形が変わらないのは、 


ex
が有名ですね。eというのは自然対数の底でe=2.7182818...です。 高校の時「フナーハチニハチイチハチ・・・」などとゴロで 暗記した記憶はありませんか？（えっ？そんなの知らないって？）

そこで、f(x)=ex

とおき、x=1を代入するとどうなるでしょう。


e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + ･･･
となります。これは電卓で計算できます。 まず、１をメモリーに入れます。次にこれを１で割った値を メモリーにいれます(M+)。次にこれを２で割ります。 この値をM+します。次にこれを３で割ります。M+します。 ４で割ります。M+します。こうしていって表示される値が ０になったらメモリー・コールボタンを押せばeの値の 近似値が求められます。（今の計算の意味が分かったでしょうか？） ちなみに、手元にある電卓で今の計算を実行すると 2.7182814となります。これをコンピュータにやらせてみましょう。

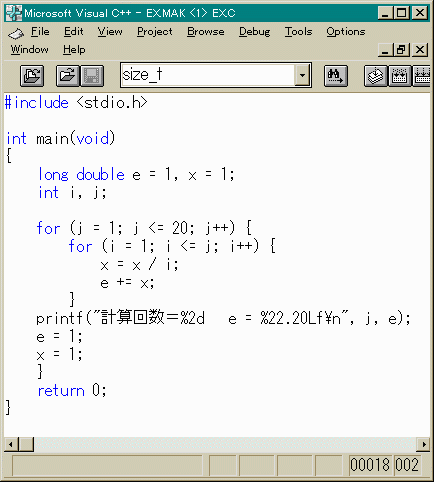jで計算回数を増やしていきます。 x は階乗の逆数でこれをどんどん足していけば ｅの値に近づきます。 １回計算が終わった時点でeやxを１に戻すのを忘れては いけません。

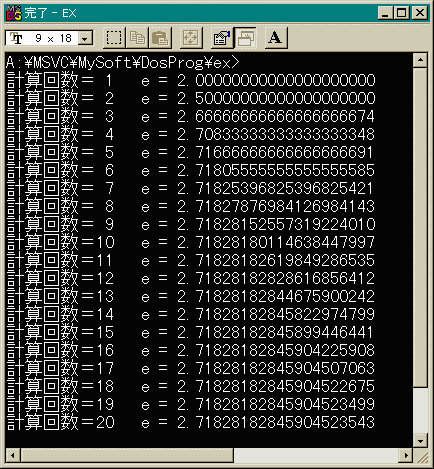
小数点以下２０桁まで計算させていますが、 計算回数を増やせばいくらでも近似値が 得られるかというとそうではありません。

ある資料によると
e=2.718281828459045235360287471352662497.....
だそうです。

左の計算結果では最後の下２桁あたりは怪しいですね。

じゃ、小数点以下１０００桁だの１０００００桁だのは どうやって計算するの？

はい。それには別なアルゴリズムが必要です。 多倍長演算(multiple-precision arithmetic)という方法が 有名です。しかし、これは超初心者の領域を越えるので このHPでは解説しません。興味のある人は、 参考書などで調べてみてください。たいていの入門書に 載っているはずです。

[Index][総合Index] [Previous Chapter] [Next Chapter]

Update Dec/22/1996 By Y.Kumei
当ホーム・ページの一部または全部を無断で複写、複製、 転載あるいはコンピュータ等のファイルに保存することを禁じます。